1343. Bad substring
Find the number of strings
of length n consisting of only the
characters ‘a’, ‘b’ and ‘c’, not containing
the substring “ab”.
Input. One integer n (0 ≤ n ≤ 45).
Output. Print the number of required strings.
|
Sample
input 1 |
Sample output 1 |
|
1 |
3 |
|
|
|
|
Sample
input 2 |
Sample output 2 |
|
3 |
21 |
SOLUTION
recurrent relation
Algorithm analysis
Let f(n) be the number of required strings of length n. If n = 1 we have 3 such strings, when n = 2 we have 8 strings:
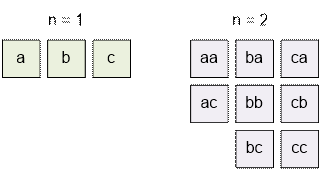
Consider all possible ways
to build the required strings. In the first position we can put one
of three letters: ‘a’, ‘b’ or ‘c’.
If we first
put ‘b’ or ‘c’, then in the next n – 1 positions we can put any of f(n – 1) words. If we first put ‘a’, then we need to consider the cases of
placing the letters in the second position. If we place in the second position ‘c’, then in the next n – 2 positions we can put any
of f(n – 2) words. If we put in the second
position ‘a’, then similarly we need to consider
the placement of letters in the third position.

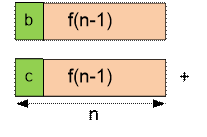





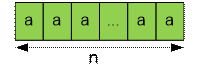
We have a relation:
f(n) = 2f(n – 1) + f(n – 2) + f(n – 3) + … + f(1) + f(0) + 1
At the same time
f(n – 1) = 2f(n – 2) + f(n – 3) + f(n – 4) + … + f(1) + f(0) + 1,
whence
f(n – 2) + f(n – 3) + f(n – 4) + … + f(1) + f(0) + 1 = f(n – 1) –
f(n – 2)
Substitute this sum in the
first relation:
f(n) = 2f(n – 1) + f(n – 1) –
f(n – 2) = 3f(n – 1) –
f(n – 2)
So we get the recurrence
relation:
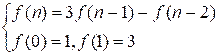
Algorithm realization
The values of function f(i) will be stored in cells f[i].
#define MAX 46
long long f[MAX];
Calculate the values f(i) (0 ≤ i ≤ MAX) by the
formula given in the algorithm analysis.
f[0] = 1; f[1] = 3;
for(i = 2; i < MAX; i++)
f[i] = 3 * f[i-1] - f[i-2];
Read the input value n
and print the result.
scanf("%d",&n);
printf("%lld\n",f[n]);
Realization with memorization
#include <stdio.h>
#include <string.h>
#define MAX 46
long long m[MAX];
int i, n;
long long f(int n)
{
if (n == 0) return 1;
if (n == 1) return 3;
if (m[n] !=
-1) return m[n];
return m[n] =
3 * f(n-1) - f(n-2);
}
int main(void)
{
scanf("%d",&n);
memset(m,-1,sizeof(m));
printf("%lld\n",f(n));
return 0;
}
Java realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
long f[] = new long[46];
f[0] = 1; f[1] = 3;
for(int i = 2; i < 46; i++)
f[i] = 3 * f[i-1] - f[i-2];
System.out.println(f[n]);
con.close();
}
}
Java realization –
recursion with memorization
import java.util.*;
public class Main
{
static long m[] = new long[46];
static long f(int n)
{
if (n == 0) return 1;
if (n == 1) return 3;
if (m[n] != -1) return m[n];
return m[n] = 3 * f(n-1) - f(n-2);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
Arrays.fill(m, -1);
int n = con.nextInt();
System.out.println(f(n));
con.close();
}
}
Python realization with a list
n = int(input())
res = [1,3]
for i in range(2,46):
res += [3 * res[i-1] - res[i-2]]
print (res[n])
Python realization with memorization
res = {0:1,1:3}
def f(n):
if not n in res:
res[n] = 3*f(n-1) -
f(n-2)
return res[n]
n = int(input())
print(f(n))